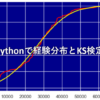
Pythonで「ヒストグラム+正規分布の近似曲線」を作成する4通りの方法

ヒストグラムは統計でデータ処理する際に使われる最も重要なグラフの一つですが、折れ線グラフや棒グラフと違って作成するのに少しテクニックが必要です。
それは一旦、元データを階級に分ける必要があることと、階級の分け方によってもグラフの形が異なってくるためです。

これは3つの階級に分けた場合のヒストグラムですが、5つの階級に分けた場合は次のようになります。

更にヒストグラムに正規分布の近似曲線を重ねて表示したい場合もあり、それには更にテクニックが必要です。

これをExcelで作成するためのテクニックについては、Excelでヒストグラムを描く二通りの方法。正規分布の近似曲線も併せて表示!で紹介しています。
今回はそのPython版です。
Matplotlib、Pandas、Seabornを使って作成してみました。
これらのライブラリーにはヒストグラムを作成する関数があるため、比較的簡単に作成できます。
そこで最後にヒストグラムにについての理解を深めるため、元データを自分で階級別に分け、それを棒グラフにする方法でもヒストグラムを作成してみました。
元データ
ある商品の91日間の出荷データをcsv形式にしたファイルを元データとしました。
ファイル名は’Shipping_data0.csv’です。

Matplotlibの関数を使う方法
ヒストグラムを描く
一番ベーシックな方法です。
Pandasでcsvファイルをデータフレームに読み込んで、そのデータをMatplotlibのhistメソッドに引数として入れるだけです。
データはデータフレーム形式のままです。
import matplotlib.pyplot as plt
import pandas as pd
data = pd.read_csv('Shipping_data0.csv')
plt.hist(data, bins=10, density=True)
plt.show()
引数はいろいろと設定できるようになっていますが、最低限必要なのはデータの他にbinとdensityです。
binでは階級の数を指定します。
ここでは10を指定しています。
この例では91個のデータの最小値が2184、最大値が69028ですので、1つの階級の幅は
(69028 – 2184) / 10 = 6684
になります。
densityでは縦軸を度数で表すか確率密度で表すかを、FalseかTrueで指定します。
冒頭の例では3つの階級に分けました。
そして1つ目の階級には4個のデータが、2つ目の階級には11個のデータが、3つ目の階級には4個のデータが含まれていました。
この4、11、4が度数になります。
確率密度については後ほど詳しく触れますが、正規分布の近似曲線を重ねて描く場合には、縦軸は確率密度で表す必要があります。
なぜならよく目にする正規分布のグラフは確率密度関数だからです。
従って、今回はdensity = Trueとしています。
コードを実行するとこのように表示されます。

正規分布の近似曲線を描く
次に正規分布の近似曲線を作成します。
正規分布は平均と標準偏差が分かれば一意に決まるので、まずはそれを計算します。
これはPandasの関数で次のように求めることができます。
mean, std = data.mean(), data.std()
次に、先のヒストグラムに重ねて近似曲線を描き入れるために、近似曲線を描く横軸の範囲を決めます。
つまりデータの最小値と最大値を求めるのですが、これもPandasの関数を使って取得できます。
xmin, xmax = data.min(), data.max()
正規分布の近似曲線は沢山の点をつなぎ合わせて描くので、次に最小値と最大値の間に等間隔に沢山の点を生成します。
これはNumpyのlinespace関数を使います。
100個の点をx_axisという名のリストに入れる場合は次のように書きます。
x_axis = np.linspace(xmin, xmax, 100)
これら100個の点は横軸上の点ですので、次にこれらに対応する縦軸上の点を求めます。
これは横軸の100個の値をそれぞれ正規分布の式に代入すれば計算できますが、Scipyのstatsモジュールにあるnorm.pdfメソッドを使えば次のように簡単に計算できます。
pdf = norm.pdf(x_axis, mean, std)
後はmatplotlibでx_axisとpdfを普通にプロットすれば、次のような正規分布近似曲線を作成できます。

ヒストグラムと正規分布近似曲線を重ね合わせる
ここまでできれば重ね合わせることは簡単です。
ヒストグラムを描くコードの後に、正規分布近似曲線を描くコードを書けばよいだけです。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.stats import norm
data = pd.read_csv('Shipping_data0.csv')
plt.hist(data, bins=10, density=True)
mean , std = data.mean(), data.std()
xmin, xmax = plt.xlim()
x_axis = np.linspace(xmin, xmax, 100)
pdf = norm.pdf(x_axis, mean, std)
plt.plot(x_axis, pdf)
plt.show()結果はこのように表示されます。

Pandasの関数を使う方法
Pandasを使えば、データフレームにhist関数をかませるだけで、更に簡単にヒストグラムを作成できます。
import pandas as pd
data = pd.read_csv('Shipping_data0.csv')
data.hist(bins=10, density=True)
正規分布近似曲線を重ね合わせるやり方も、先ほどとほぼ同じです。
違いは近似曲線を先に、ヒストグラムを後に描くことです。
import matplotlib.pyplot as plt
import pandas as pd
from scipy.stats import norm
data = pd.read_csv('Shipping_data0.csv')
xmin, xmax = data.Item_A.min(), data.Item_A.max()
mean, std = data.Item_A.mean(), data.Item_A.std()
x_axis = np.linspace(xmin, xmax, 100)
pdf = norm.pdf(x_axis, mean, std)
pdf_graph = pd.DataFrame({"X":x_axis, "norm":pdf}).set_index("X")
pdf_graph.plot()
data.Item_A.hist(bins=10, density=True)
Seabornの関数を使う方法
Seabornを使っても、Matplotlibと同じように作成できます。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from scipy.stats import norm
data = pd.read_csv('Shipping_data0.csv')
graph = sns.histplot(data, bins = 10, stat = 'density')
xmin, xmax = data.min(), data.max()
mean, std = data.mean(), data.std()
x_axis = np.linspace(xmin, xmax, 100)
pdf = norm.pdf(x_axis, mean, std)
graph.plot(x_axis, pdf)
棒グラフで自作する方法
このようにライブラリーを使えば簡単に「ヒストグラム+正規分布の近似曲線」を作成できますが、ヒストグラムがどういうものであるのかを理解するために、一から自作してみましょう。
基本的にヒストグラムは棒グラフですので、棒グラフを使って作成してみます。
まずはデータフレームをnumpyで扱えるようにndarrayに変換します。
data = pd.read_csv('Shipping_data0.csv')
data_arr = data.to_numpy().reshape(91,)
次に10個の階級を作ります。
先ほど使ったlinespace関数で最小値と最大値の間を均等に10個の箱(階級)に区切ります。
xmin, xmax = data_arr.min(), data_arr.max()
xcnt = data_arr.shape
number_of_bins = 10
bin_list = np.linspace(xmin, xmax, number_of_bins + 1)
最後で箱の数に1を足しています。
これはlinespace関数で発生させる点は箱を区切る数字であるため、箱が10個必要であれば区切る数字は11個必要であるためです。

次に各箱に入るデータの数を計算します。
それにはnumpyのhistogram関数を使えば、次のようにhistという名のリストに返してくれます。
hist,bins = np.histogram(data_arr, bins = bin_list)
次に各箱(階級)を代表する数値を計算します。
各箱は○○~××のように範囲を表しているため、〇〇と××の平均値を計算します。

やり方はいくつかあると思いますが、ここでは先ほど生成した11個の値が入ったhistという名のリストを、1つずつ要素をずらしたリストをまず作り、これら2つのリストの平均を計算することにします。

次のようにコーディングすることでaveという名のリストに格納されます。
但し11個目の要素は箱の代表値としては不要なので削除します。
bins_slide = np.roll(bins, -1)
ave = (bins + bins_slide)/2
ave = ave[:-1]
最後に度数を確率密度に変換します。
リストhistには各箱(階級)に含まれるデータの個数(度数)が入っていますので、それを確率密度に変換します。
そのためには次の2つのステップを踏みます。
ステップ1)
度数を相対度数に変換する。
例えば、ある階級に属するデータ数が5だとすれば、全体のデータ数は91ですので、5 / 91 = 0.055が相対度数になります。
ステップ2)
相対度数を確率密度に変換する。
例えば各階級を1000~2000、2000~3000、・・・のように1000の幅で区切っている場合、相対度数を階級幅で割ることにより確率密度が計算されます。
相対度数が0.055、階級幅が1000である場合、確率密度は0.000055になります。
従って、次のようにコーディングすることにより、リストhistに各階級の確率密度が格納されます。
width_actual = ave[1] - ave[0]
hist = hist / xcnt / width_actual
あとはmatplotlibを使ってaveを横軸に、histを縦軸に棒グラフをプロットするだけです。
ヒストグラムっぽくするために、棒の幅を階級幅に指定して、棒間の間隔がゼロになるように引数で設定します。
plt.bar(ave, hist, width = width_actual)
このように全く同じヒストグラムを作成することができました。

ここまでできれば、先ほどと同じように正規分布を描くコードを後に付け加えることによって、正規分布近似曲線を重ね合わせることができます。
import numpy as np
import matplotlib.pyplot as plt
data = pd.read_csv('Shipping_data0.csv')
data_arr = data.to_numpy().reshape(91,)
xmin, xmax = data_arr.min(), data_arr.max()
number_of_bins = 10
bin_list = np.linspace(xmin, xmax, number_of_bins + 1)
hist,bins = np.histogram(data_arr, bins = bin_list)
bins_slide = np.roll(bins, -1)
bins_ave = (bins + bins_slide)/2
bins_ave = bins_ave[:-1]
width_actual = bins_ave[1] - bins_ave[0]
xcnt = data_arr.shape
hist = hist / xcnt / width_actual
plt.bar(bins_ave, hist, width = width_actual)
mean = data_arr.mean()
std = data_arr.std()
xmin, xmax = plt.xlim()
x_axis = np.linspace(xmin, xmax, 100)
pdf = norm.pdf(x_axis, mean, std)
plt.plot(x_axis, pdf)
plt.show()